Επιστήμη - Επιστημολογία
- Το θεώρημα της μη πληρότητας και φιλοσοφικές προεκτάσεις
- Η ελευθερία του απροσδιόριστου
- Σχετικότητα και προεκτάσεις
- Θεωρία της σχετικότητας: οι έννοιες
- Κβαντομηχανική: έννοιες και ερμηνευτικά ρεύματα
- Eρμηνείες της κβαντoμηχανικής: Ο Schrodinger και η γάτα του
- Προς μια θεωρία των πάντων
- Οικοσύνθεση στον Άρη
- Διαλεκτική βιολογία
- Οι αντιλήψεις του Schrodinger για το "Τι είναι η ζωή"
Θεωρία της σχετικότητας: οι έννοιες
Πρόλογος
 Ήταν γύρω στο 1900, όταν ο Kelvin διακήρυξε ότι «Η Φυσική έχει πια λύσει τα θεμελιακά προβλήματα. Από τώρα και μπρος δεν θα είναι παρά απλή εφαρμογή των γενικών νόμων. Μένουν βέβαια μερικά θεματάκια που δεν τα έχουμε κατανοήσει πλήρως: την κατανομή του μέλανος σώματος, οι φασματικές γραμμές των αερίων…». Δεν θα μπορούσε να φανταστεί, τότε, ότι τέτοια «θεματάκια» θα ανέτρεπαν, μέσα στα επόμενα χρόνια, εκ θεμελίων το πώς αντιλαμβανόμαστε τη φύση.
Ήταν γύρω στο 1900, όταν ο Kelvin διακήρυξε ότι «Η Φυσική έχει πια λύσει τα θεμελιακά προβλήματα. Από τώρα και μπρος δεν θα είναι παρά απλή εφαρμογή των γενικών νόμων. Μένουν βέβαια μερικά θεματάκια που δεν τα έχουμε κατανοήσει πλήρως: την κατανομή του μέλανος σώματος, οι φασματικές γραμμές των αερίων…». Δεν θα μπορούσε να φανταστεί, τότε, ότι τέτοια «θεματάκια» θα ανέτρεπαν, μέσα στα επόμενα χρόνια, εκ θεμελίων το πώς αντιλαμβανόμαστε τη φύση.
Η Φυσική ήταν πράγματι στις δόξες της στο τέλος του 19ου αιώνα. Ένα οικοδόμημα λιτό, κομψό και με μεγάλη εμβέλεια και βάθος ερμηνευτικής ισχύος. Η εξίσωση του Νεύτωνα (F=ma) καθόριζε την κίνηση υλικών σημείων και σωμάτων. Οι δυνάμεις F που προκαλούσαν την κίνηση ήταν, σε τελευταία ανάλυση, είτε βαρυτικές, είτε ηλεκτρομαγνητικές. Οι ηλεκτρομαγνητικές δυνάμεις διαδίδονταν με την ταχύτητα του φωτός, υπό μορφή κύματος και το φως ήταν μια ειδική περίπτωση διαδιδόμενου ηλεκτρομαγνητικού κύματος.
Η ύλη αποτελείτο από στοιχειώδη σωμάτια που συγκροτούνται μεταξύ τους λόγω αμοιβαίων ηλεκτρομαγνητικών δυνάμεων και οι ιδιότητες της ύλης μπορούσαν να ερμηνευτούν σαν αποτέλεσμα της μικροσκοπικής κίνησης των στοιχειωδών σωματιδίων.
Το μέλλον, λοιπόν, της φυσικής φάνταζε μάλλον μονότονο: Απλή εφαρμογή γνωστών κανόνων. Όμως κάτω από την επιφάνεια της πλήρους επιτυχίας, διαφαίνονταν κάποιες «ρωγμές» που σύντομα θα επέβαλαν την εκ βάθρων εννοιολογική αναδόμηση του κλασικού οικοδομήματος.
Σε αυτήν την εργασία προσεγγίζονται οι νέες έννοιες που εισήγαγε η θεωρία της σχετικότητας. Στον ιστότοπο αυτό μπορείτε να διαβάσετε και για τις νέες έννοιες που εισήγαγε και η κβαντομηχανική όσο και μια εισαγωγή στο όνειρο των φυσικών για την ανάπτυξη μιας ενιαίας θεωρίας των πάντων.
1) Η ειδική θεωρία της σχετικότητας
 Το 1905 ο Einstein, βασιζόμενος στα νέα πειραματικά δεδομένα και υπερβαίνοντας τις κλασικές προκαταλήψεις, έφερε δύο νέες παραδοχές:
Το 1905 ο Einstein, βασιζόμενος στα νέα πειραματικά δεδομένα και υπερβαίνοντας τις κλασικές προκαταλήψεις, έφερε δύο νέες παραδοχές:
1. Η ταχύτητα του φωτός στο κενό είναι ίδια σε όλα τα συστήματα συντεταγμένων (Σ.Σ.) που βρίσκονται σε σχετική ομαλή κίνηση.
2. Όλοι οι νόμοι της φύσης είναι ίδιοι σε όλα τα Σ.Σ. που βρίσκονται σε σχετική ομαλή κίνηση.
Αυτές οι παραδοχές βρίσκονται σε αντίθεση με τους κλασικούς μετασχηματισμούς οι οποίοι πρέπει να αντικαταστούν. Τροποποιήσεις στις (1) και (2) οδηγούν σε αντίθεση με το πείραμα κι επομένως πρέπει να αποδεχτούμε την ισχύ τους και να αναθεωρήσουμε, τον τρόπο με τον οποίο μετασχηματίζονται οι θέσεις και οι ταχύτητες κατά τα πέρασμα από ένα Σ.Σ. σε άλλο. Σκοπός είναι να βγάλουμε συμπεράσματα από την (1) και (2), να δούμε πού και πώς αυτές οι παραδοχές έρχονται σε αντίθεση με τους κλασικούς μετασχηματισμούς, και να βρούμε τη φυσική σημασία των αποτελεσμάτων πού θα πετύχουμε.
Θα χρησιμοποιήσουμε το παράδειγμα ενός κινούμενου δωματίου με έναν εσωτερικό και έναν εξωτερικό παρατηρητή που κινείται κάθετα στους τοίχους. Αν εκπέμπεται ένα φωτεινό σήμα από το κέντρο του δωματίου, ρωτάμε τους δυο ανθρώπους τι περιμένουν να παρατηρήσουν, αν έχουν στο μυαλό τους μονάχα τις δυο αρχές.
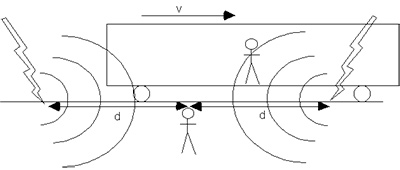 Ο εσωτερικός παρατηρητής: Το φωτεινό σήμα που προχωρεί από το κέντρο του δωματίου θα φτάσει ταυτόχρονα στους δυο τοίχους, εφόσον απέχουν το ίδιο από τη φωτεινή πηγή και η ταχύτητα του φωτός είναι η ίδια προς όλες τις κατευθύνσεις.
Ο εσωτερικός παρατηρητής: Το φωτεινό σήμα που προχωρεί από το κέντρο του δωματίου θα φτάσει ταυτόχρονα στους δυο τοίχους, εφόσον απέχουν το ίδιο από τη φωτεινή πηγή και η ταχύτητα του φωτός είναι η ίδια προς όλες τις κατευθύνσεις.
Ο εξωτερικός παρατηρητής: Στο σύστημα μου η ταχύτητα του φωτός είναι ακριβώς η ίδια με την ταχύτητα στο σύστημα του παρατηρητή που κινείται με το δωμάτιο. Αυτό που βλέπω είναι ένα φωτεινό σήμα που διαδίδεται με μια σταθερή ταχύτητα, ίδια προς όλες τις κατευθύνσεις. Ο ένας τοίχος απομακρύνεται, από το φωτεινό σήμα, ο άλλος το πλησιάζει. Γι' αυτόν το λόγο, το φως θα συναντήσει λίγο πιο αργά τον τοίχο που απομακρύνεται, παρά τον τοίχο που πλησιάζει.
Συγκρίνοντας τις προβλέψεις των παρατηρητών μας, βρίσκουμε ένα συμπέρασμα που έρχεται σε αντίθεση με τις έννοιες της κλασικής φυσικής. Δυο γεγονότα, δηλ. οι δυο φωτεινές ακτίνες που χτυπούν τους δυο τοίχους, είναι σύγχρονα για τον εσωτερικό παρατηρητή, όχι όμως και για τον εξωτερικό.
Στην κλασική φυσική είχαμε ένα ρολόι μονάχα, μια μοναδική ροή του χρόνου για όλους τους παρατηρητές, σε όλα Σ.Σ. Ο χρόνος, και κατά συνέπεια εκφράσεις όπως, «ταυτόχρονα», «νωρίτερα», «αργότερα», είχαν μια σημασία απόλυτα ανεξάρτητη από οποιοδήποτε Σ.Σ.
Η θεωρία της σχετικότητας μας υποχρεώνει να εγκαταλείψουμε αυτή την άποψη. Και πρέπει να κατανοήσουμε τη σημασία της πρότασης: «Δυο γεγονότα πού είναι σύγχρονα σε ένα Σ.Σ., μπορεί να μην είναι σύγχρονα σε ένα άλλο Σ.Σ.». Πριν από αυτό, όμως, πρέπει να εξηγήσουμε τι εννοούμε με το «δυο γεγονότα σύγχρονα σε ένα Σ.Σ.».
Για να συζητήσουμε αυτά χρειαζόμαστε ρολόγια. Οποιοδήποτε φυσικό φαινόμενο μπορεί να χρησιμέψει για ρολόι, φτάνει να επαναλαμβάνεται με ακρίβεια όσες φορές θελήσουμε.
Ας θεωρήσουμε πως σε δυο σημεία που απέχουν μεταξύ τους, έχουμε τοποθετήσει δυο τέλεια ρολόγια, που δείχνουν ακριβώς την ίδια ώρα. Πώς μπορούμε να είμαστε βέβαιοι, πως δυο απομακρυσμένα ρολόγια δείχνουν ακριβώς την ίδια ώρα; Θα μπορούσαμε να τοποθετηθούμε σ' ένα σημείο πού να απέχει το ίδιο κι από τα δυο ρολόγια, και να παρατηρούμε σ' αυτό το σημείο τα είδωλα τους πού μεταδίδονται από μια τηλεόραση που ισαπέχει από τα δύο. Αν τα δυο σήματα εκπέμπονται ταυτόχρονα, θα φτάσουνε σε μένα την ίδια στιγμή. Αν δυο «καλά» ρολόγια πού παρατηρούνται από τη μέση της απόστασης πού τα χωρίζει δείχνουν πάντα την ίδια ώρα, τότε είναι κατάλληλα για να δείχνουν την ώρα σε δυο σημεία απομακρυσμένα μεταξύ τους.
Ωστόσο το να χρησιμοποιούμε μονάχα ένα ρολόι δεν μας εξυπηρετεί, γιατί είμαστε υποχρεωμένοι να κάνουμε όλες μας τις μετρήσεις κοντά του. Παρατηρώντας από μακριά το ρολόι, π.χ. μέσω της τηλεόρασης, πρέπει πάντα να 'χουμε στο μυαλό μας, πώς εκείνο πού βλέπουμε τώρα, έγινε στην πραγματικότητα πρωτύτερα. Είμαστε υποχρεωμένοι να κάνουμε διορθώσεις σ' όλες μας τις χρονικές μετρήσεις, ανάλογα με την απόσταση μας από το ρολόι.
Δε βολεύει λοιπόν να έχουμε μονάχα ένα ρολόι. Αλλά μια και ξέρουμε τώρα πώς να ξεκαθαρίσουμε αν δυο ή περισσότερα ρολόγια δείχνουν την ίδια ώρα και δουλεύουν με τον ίδιο ρυθμό, μπορούμε να φανταστούμε όσα ρολόγια θέλουμε μέσα σ' ένα δοσμένο Σ.Σ. Καθένα τους θα μας βοηθά να καθορίζουμε το χρόνο των γεγονότων πού συμβαίνουν στην άμεση γειτονιά του. Όλα τα ρολόγια ηρεμούν σε σχέση με το Σ.Σ. Είναι «καλά» και συγχρονισμέναρολόγια, που σημαίνει πώς δείχνουν την ίδια ώρα.
Τα γεγονότα είναι σύγχρονα αν τα συγχρονισμένα ρολόγια που βρίσκονται κοντά τους, δείχνουν την ίδια ώρα, τη στιγμή που παράγονται. Το να λέμε πως ένα από τα απομακρυσμένα γεγονότα συνέβη πριν από το άλλο, έχει τώρα καθορισμένο νόημα.
Για να διαπραγματευθούμε το πρόβλημα δυο συστημάτων που βρίσκονται σε σχετική ομαλή κίνηση, πρέπει να θεωρήσουμε δυο ράβδους, εφοδιασμένες με ρολόγια. Ο παρατηρητής σε καθένα απ' αυτά τα δυο Σ.Σ., έχει τώρα τη δική του ράβδο και τη δική του σειρά ρολογιών σταθερά δεμένων μ' αυτήν.
Όταν διαπραγματευτήκαμε το ζήτημα των μετρήσεων στην κλασική μηχανική, χρησιμοποιήσαμε μονάχα ένα ρολόι, για όλα τα Σ.Σ. Εδώ έχουμε πολλά ρολόγια για κάθε Σ.Σ. Η διαφορά αυτή δεν έχει σημασία. Ωστόσο κανείς δε μπορεί να έχει αντίρρηση (για λόγους ευκολίας) στη χρησιμοποίηση των πολλών, φτάνει να συμπεριφέρνονται σαν καλά συγχρονισμένα ρολόγια.
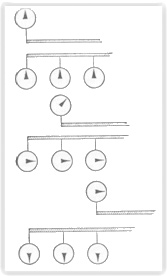
Τώρα πλησιάζουμε τo σημείο που φανερώνει πού έρχονται σε αντίθεση οι κλασικοί μετασχηματισμοί με τη θεωρία της σχετικότητας. Τι συμβαίνει όταν δυο σειρές ρολόγια κινούνται ομαλά, η μια σε σχέση με την άλλη; Ο κλασικός φυσικός θα απαντούσε: τίποτα.
Ωστόσο θα μπορούσαμε να φανταστούμε κι ένα κινούμενο ρολόι που προχωρεί με διαφορετικό ρυθμό από ένα ακίνητο. Ας συζητήσουμε αυτή τη δυνατότητα. Τι εννοούμε λέγοντας πως ένα ρολόι που κινείται αλλάζει ρυθμό; Ας δεχτούμε, για λόγους απλότητας, πως έχουμε μονάχα ένα ρολόι στο επάνω Σ.Σ. και πολλά στο κάτω. Όλα τα ρολόγια έχουν τον ίδιο μηχανισμό και τα κάτω είναι συγχρονισμένα. Σχεδιάσαμε τρεις διαδοχικές θέσεις των δυο Σ.Σ. πού κινούνται ομαλά το ένα σε σχέση με το άλλο. Στο πρώτο σχήμα, οι δείκτες του επάνω και των κάτω ρολογιών βρίσκονται στην ίδια θέση, γιατί έτσι τους βάλαμε. Όλα τα ρολόγια δείχνουν την ίδια ώρα. Στο δεύτερο σχέδιο βλέπουμε τις σχετικές θέσεις των δυο Σ.Σ. υστέρα από κάποιο χρόνο.
Όλα τα ρολόγια στο κάτω Σ.Σ. δείχνουν ιδίαν ώρα, αλλά το ρολόι στο επάνω Σ.Σ. δεν προχωρεί πια με τον ίδιο ρυθμό. Ο ρυθμός άλλαξε και η ώρα είναι διαφορετική, γιατί το ρολόι κινείται σχετικά με το κάτω Σ.Σ. Στο τρίτο σχήμα, βλέπουμε πώς η διαφορά των θέσεων των δεικτών αυξάνει με τον χρόνο.
Ένας παρατηρητής που βρίσκεται ακίνητος στο κάτω Σ.Σ. θα ‘βρισκε πως ένα ρολόι που κινείται, μεταβάλλει ρυθμό. Στο ίδιο αποτέλεσμα θα έφτανε κανείς αν το ρολόι κινιότανε σχετικά μ' ένα παρατηρητή ακίνητο στο πάνω Σ.Σ. Σ' αυτή την περίπτωση θα 'πρεπε να υπάρχουν πολλά ρολόγια στο πάνω Σ.Σ., και ένα μονάχα στα κάτω. Οι νόμοι της φύσης πρέπει να είναι ίδιοι στα δυο Σ.Σ.
Στην κλασική μηχανική, λοιπόν, γινόταν δεκτό σιωπηρά, πως ένα κινούμενο ρολόι δεν αλλάζει το ρυθμό του. Ωστόσο μπορούμε να φανταστούμε πως ένα κινούμενο ρολόι μεταβάλλει ρυθμό, εφόσον ο νόμος αυτής της αλλαγής είναι ο ίδιος για όλα τα συστήματα αδράνειας.
Ας μελετήσουμε τώρα και το μήκος. Ας πάρουμε μια ράβδο με μήκος ένα μέτρο. Αυτό σημαίνει πως έχει μήκος ένα μέτρο, εφ' όσον ηρεμεί σε ένα Σ.Σ. Ας υποθέσουμε τώρα πως κινείται ομαλά, γλιστρώντας κατά μήκος της ράβδου που αντιπροσωπεύει το Σ.Σ. Το μήκος της θα φαίνεται ότι είναι πάντα ένα μέτρο; Πρώτα πρέπει να ξέρουμε πώς να προσδιορίσουμε το μήκος της όταν βρίσκεται σε κίνηση. Αυτό μπορεί να γίνει με τον ακόλουθο τρόπο: Σε μια δοσμένη στιγμή, δυο παρατηρητές φωτογραφίζουν ταυτόχρονα, ο ένας την αρχή κι ο άλλος το τέλος της. Αφού οι εικόνες πάρθηκαν ταυτόχρονα, μπορούμε να συγκρίνουμε πάνω στη ράβδο που παριστάνει το Σ.Σ., τα σημάδια με τα οποία συμπίπτουν η αρχή και το τέλος της ράβδου.
Χρειαζόμαστε δυο παρατηρητές για να σημειώσουν σύγχρονα γεγονότα σε διαφορετικές θέσεις ενός δοσμένου Σ.Σ. Αφού οι φωτογραφίες πρέπει να παρθούν ταυτόχρονα και το «ταυτόχρονα» είναι μια σχετική έννοια πού εξαρτάται από το Σ.Σ., φαίνεται δυνατό να είναι διαφορετικά τα αποτελέσματα αυτών των μετρήσεων, σε διαφορετικά Σ.Σ. πού βρίσκονται σε σχετική κίνηση.
Γνωρίζουμε ότι η ταχύτητα του φωτός, είναι ίδια σ' όλα τα συστήματα αδράνειας. Είναι αδύνατο να συμφιλιώσουμε το γεγονός αυτό, με τους κλασικούς μετασχηματισμούς. Ο κύκλος των παραδοχών μας πρέπει να σπάσει σε κάποιο σημείο. Μήπως αυτό μπορεί να γίνει σε τούτο ακριβώς το σημείο; Μήπως δηλαδή μπορούμε να δεχτούμε αλλαγές στο ρυθμό του κινούμενου ρολογιού και στο μήκος της κινούμενης ράβδου, τέτοιες ώστε η σταθερότητα της ταχύτητας του φωτός να είναι άμεσο επακόλουθο τους;
Το επιχείρημα μπορεί και να αντιστραφεί: αν η ταχύτητα του φωτάς είναι ίδια σ' όλα τα Σ.Σ., τότε κινούμενες ράβδοι πρέπει να μεταβάλλουν τα μήκη τους και κινούμενα ρολόγια πρέπει να μεταβάλλουν το ρυθμό τους.
Αυτά μπορεί να φαίνονται περίεργα, αλλά από τη σκοπιά της θεωρίας της σχετικότητας, οι αντιλήψεις της κλασικής φυσικής φαίνονται αυθαίρετες. Γιατί να πιστεύουμε στον απόλυτο χρόνο, που ρέει με τον ίδιο τρόπο για όλους τους παρατηρητές, σε όλα τα Σ.Σ.; Γιατί να πιστεύουμε πως η απόσταση είναι αμετάβλητη; Οχρόνος καθορίζεται από ρολόγια, οι συντεταγμένες του χώρου από ράβδους και το αποτέλεσμα του καθορισμού τους εξαρτάται από τη συμπεριφορά αυτών των ρολογιών και των ράβδων, όταν βρίσκονται σε κίνηση.
Άλλωστε οι εξισώσεις Maxwell δεν είναι αναλλοίωτες σε σχέση με τους κλασικούς μετασχηματισμούς. Αυτό υποδεικνύει πως η σύνδεση ανάμεσα σε δυο Σ.Σ. πρέπει να είναι διαφορετική. Απεναντίας, οι εξισώσεις Maxwell, είναι αναλλοίωτες σε σχέση με τους μετασχηματισμούς Lorentz οι οποίοι περιλαμβάνουν και νόμους μετασχηματισμού για το χρόνο. Στην κλασική φυσική είχαμε νόμους μετασχηματισμού για τις συντεταγμένες και για τις ταχύτητες, αλλά οι νόμοι της μηχανικής ήταν ίδιοι για δυο Σ.Σ. που βρισκότανε σε σχετική ομαλή κίνηση. Είχαμε νόμους μετασχηματισμού για το χώρο, όχι όμως και για το χρόνο, γιατί ο χρόνος ήταν ο ίδιος για όλα τα Σ.Σ. Τα πράγματα είναι διαφορετικά στη θεωρία της σχετικότητας: Έχουμε νόμους μετασχηματισμού για το χώρο, το χρόνο και την ταχύτητα, διαφορετικούς από της κλασικής μηχανικής.
Και πάλι, οι νόμοι της φύσης πρέπει να είναι ίδιοι για όλα τα Σ.Σ. πού βρίσκονται σε ομαλή σχετική κίνηση. Σ' όλα τα συστήματα αδράνειας ισχύουν οι ίδιοι νόμοι και το πέρασμα από το ένα στο άλλο γίνεται με τους μετασχηματισμούς του Lorentz.
Από αυτούς συνάγεται πως μια κινούμενη ράβδος συστέλλεται προς την κατεύθυνση της κίνησης και η συστολή μεγαλώνει με την αύξηση της ταχύτητας. Δεν υπάρχει όμως συστολή κατά τη διεύθυνση που είναι κάθετη με τη διεύθυνση της κίνησης. Το μήκος μιας ράβδου θα 'φτάνε στο μηδέν, αν η ταχύτητα της έφτανε την ταχύτητα του φωτός. Επίσης ο ρυθμός ενός κινούμενου ρολογιού θα επιβραδυνότανε σε σύγκριση με των ρολογιών μπροστά από τα όποια περνά και θα μηδενιζόταν, αν το ρολόι έφτανε να κινείται με την ταχύτητα του φωτός. Ο αριθμός που εκφράζει την ταχύτητα του φωτός εμφανίζεται στους μετασχηματισμούς του Lorentz και παίζει το ρόλο οριακής ταχύτητας, όπως η άπειρη ταχύτητα στην κλασική μηχανική.
Μετάβαση σε άλλη ενότητα του άρθρου: